|
A displacement of
![]() in parametric latitude
along the meridional ellipse is illustrated in Figure 2.
The poleward displacement is
in parametric latitude
along the meridional ellipse is illustrated in Figure 2.
The poleward displacement is
![]() and the equatorial component is
and the equatorial component is
![]() From this we see that the geodetic and parametric latitudes are
related by
From this we see that the geodetic and parametric latitudes are
related by
![]() is the radius of curvature of the meridional arc at
is the radius of curvature of the meridional arc at ![]() . The
radius of curvature in the perpendicular plane (i.e. in the plane of the
parallel),
. The
radius of curvature in the perpendicular plane (i.e. in the plane of the
parallel), ![]() is given by
is given by
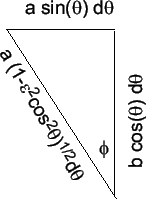
In Figure 3 we illustrate the result of a displacement of
![]() in parametric
latitude
and of
in parametric
latitude
and of ![]() in
longitude, resulting in a Northerly displacement of
in
longitude, resulting in a Northerly displacement of
![]() and an Easterly displacement of
and an Easterly displacement of
![]() , respectively.
By Pythagoras' theorem the displacement distance
, respectively.
By Pythagoras' theorem the displacement distance ![]() is
given by:
is
given by: