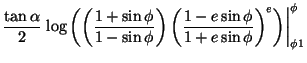 |
|||
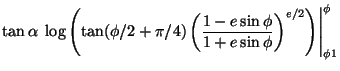 |
(8) |
Inverting this relation, to find the geodetic latitude ![]() given
the longitude
given
the longitude ![]() , can most readily be done iteratively, using:
, can most readily be done iteratively, using:
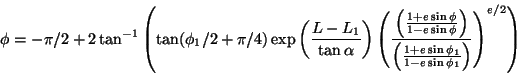 |
(9) |
Combining equations (6) and (7)
with ![]() constant gives us a differential equation for the
arc-length along the rhumb line:
constant gives us a differential equation for the
arc-length along the rhumb line:
| (10) |
| (12) |
Formally, ![]() can be expressed in terms of the elliptic
integral of the second kind
can be expressed in terms of the elliptic
integral of the second kind ![]() by[1]
by[1]
| (13) |
Expanding to ![]() ,
, ![]() is approximately given
by[4]:
is approximately given
by[4]:
| (14) |
Along a parallel, which is an E-W rhumb line, Eqns. (8)
and (11) diverge,
but since ![]() is constant, we have from Eqn. (6):
is constant, we have from Eqn. (6):
| (15) |
A map with longitude as the x-axis and ![]() as the y-axis has
a Mercator[4] projection (with the equator as the standard
parallel) on which rhumb lines plot as straight lines with the correct azimuth.
as the y-axis has
a Mercator[4] projection (with the equator as the standard
parallel) on which rhumb lines plot as straight lines with the correct azimuth.