| (23) |
| (23) |
| (24) |
In the spherical limit, ![]() , this is readily integrated to give
, this is readily integrated to give
![]() , where
, where
![]() .
. ![]() is the longitude difference, corresponding the arc-length
is the longitude difference, corresponding the arc-length ![]() on the
auxiliary sphere.
on the
auxiliary sphere.
Expanding in powers of ![]() and integrating term by term, we thus
obtain:
and integrating term by term, we thus
obtain:
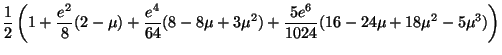 |
|||
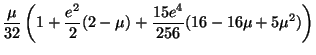 |
|||
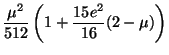 |
|||
| (26) |
Vincenty[5] has again rearranged a subset of the resulting equations into nested forms more suitable for computation:
| (28) |
As in Eqn. (22), the origins of ![]() ,
,![]() and
and
![]() have been shifted from the equator to the initial point
(1).
have been shifted from the equator to the initial point
(1). ![]() is then given by
is then given by
| (29) |