


Next: Longitude difference
Up: Geodesics on a spheroid
Previous: Geodesics on a spheroid
From Fig. 3 and Eqn. (17) we see that:
 |
(18) |
and thus
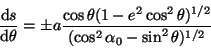 |
(19) |
with the sign being that of 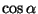 . We now substitute
. We now substitute
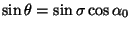 , where
, where  is the
arc-length along the great circle on the auxiliary sphere, measured
from where it crosses the equator in a Northerly direction, obtaining:
is the
arc-length along the great circle on the auxiliary sphere, measured
from where it crosses the equator in a Northerly direction, obtaining:
 |
(20) |
where
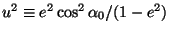 . By expanding in a power
series in
. By expanding in a power
series in 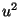 and integrating term by term[3,5], we
obtain
and integrating term by term[3,5], we
obtain 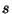 in the form:
in the form:
The distance between two points
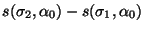 , on a geodesic arc is best obtained, after differencing
Eqn. (21), by using the identity
, on a geodesic arc is best obtained, after differencing
Eqn. (21), by using the identity
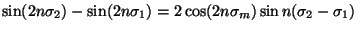 , where
, where
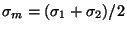 . This avoids excessive loss of
significant digits when the two points are close together.
. This avoids excessive loss of
significant digits when the two points are close together.
Vincenty[5] has rearranged a subset of the resulting equations
into
nested forms more suitable for computation:
In equations (22) the origins of 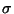 and
and 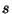 have
been shifted from the equator to the initial point (
have
been shifted from the equator to the initial point (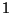 ), where the reduced
latitude is
), where the reduced
latitude is 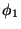 and the azimuth of the geodesic is
and the azimuth of the geodesic is 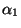 .
.



Next: Longitude difference
Up: Geodesics on a spheroid
Previous: Geodesics on a spheroid
Ed Williams
2002-03-21
![]() , on a geodesic arc is best obtained, after differencing
Eqn. (21), by using the identity
, on a geodesic arc is best obtained, after differencing
Eqn. (21), by using the identity
![]() , where
, where
![]() . This avoids excessive loss of
significant digits when the two points are close together.
. This avoids excessive loss of
significant digits when the two points are close together.